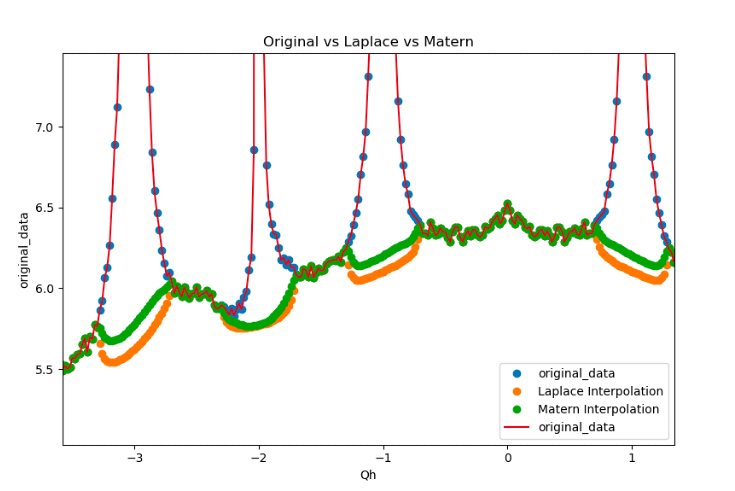
Matérn kernels are widely used due to their flexibility in describing physical datasets (thin plate splines and some radial basis functions are a special case!), however interpolation using this method has complexity O(N^3).
We have developed a fast, O(N), code for interpolating data available on a regular volumetric grid using an approximation to the Green’s function for the Matérn kernel. There are also close bounds on accuracy.
To the left is a 1D cut of a 3-dimensional scattering pattern in which spherical regions near integer (Bragg) locations have been removed and interpolated. Two parameters govern the Matérn approximation, an order parameter and a roughness parameter (1, 0.0) “Laplace” and (2, 0.0) “Matern” are shown.
The power spectrum of a physical process is a powerful tool to quantify temporal or spatial correlation. While all methods of estimating the power spectrum result in bias, the Thomson multitaper method produces a power spectrum estimate with provably improved statistical properties (lower bias, lower variance). The method hinges on the use of multiple tapers, where the taper is a sequence premultiplied by the data before the Fourier transform is applied – the taper reduces the bias of the estimator, while averaging of individual estimates reduces its variance.
This is a general purpose Julia package for analysis of univariate and multivariate time series and spatial datasets using the frequency domain. It also includes leakage-constraining tapers in multiple dimensions. It leverages the speed and ease-of-use of the Julia language to produce readable code and fast results.
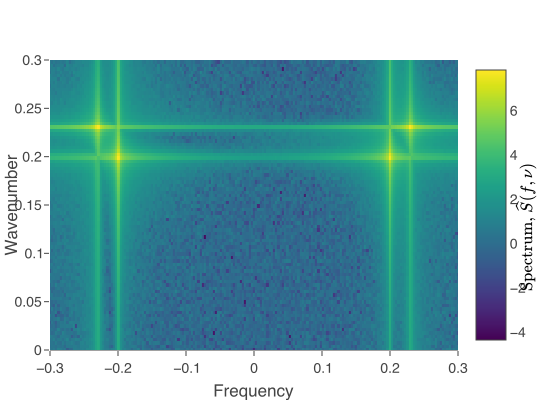
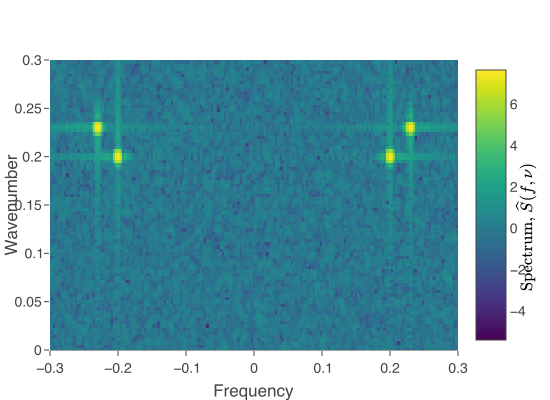
Shown on the right is the two dimensional power spectrum of a pair of standing waves using (a) conventional analysis and (b) tapered with two dimensional Cartesian discrete prolate spheroidal tapers. Much less leakage is seen with the use of the taper. Code is here. See paper.
Gaussian windowing
The analysis of pair distribution functions of x-ray scattering intensities for different crystals can sometimes benefit from premultiplying by a window function to isolate features of interest in the intensity. It turns out that the window function requires some careful thought so as not to introduce artifacts in its Fourier transformation.
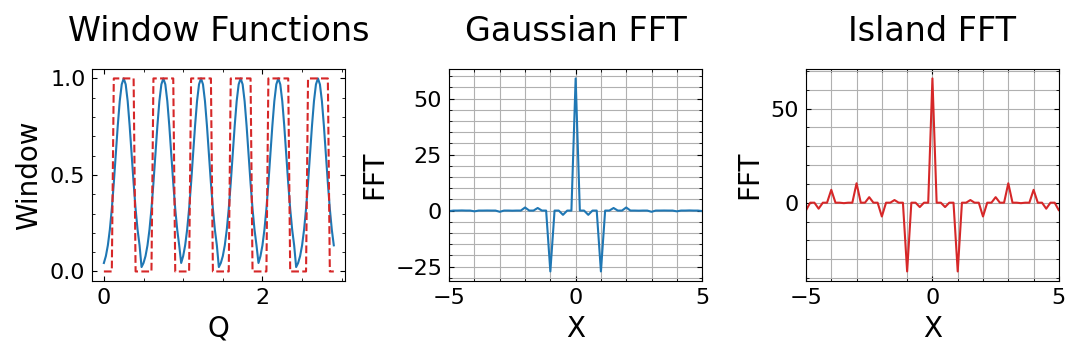
This is a tutorial-style Julia notebook that explores the Fourier transform of different window functions in three dimensions. In this particular example, we compare the three dimensional boxcar sphere with a three dimensional Gaussian window in terms of the extent of its Fourier transform. The boxcar window has a sinc kernel as its DFT while the Gaussian window has a Gaussian DFT. While the former produces oscillations that do not decay quickly away from the zero wavenumber, the latter decays much more quickly, leading to less interference between patterns in the PDF.